Algorithmische Geometrie
KE 1 - Grundlagen
Topologie
Topologie
Metrischer Raum
Wege
Zusammenhangskomponente
Graphentheorie
Graph
schlicht
kreuzungsfrei
planar
Eulersche Formel v - e + f = c + 1 (v Knoten, e Kanten, f Flächen, c Zusammenhangskomponenten)
Dualität
Geometrie
konvex
Komplexität
O(f) obere Schranke
Ω(f) untere Schranke
Θ(f) gleich große Komplexität
o(f) echt obere Schranke
Untere Schranken
Sortieren hat untere Schranke Ω(n log n ) wegen Entscheidungsbaum.
Aber kann man durch Rechnen schneller sortieren?
Der Elementtest berechnet, ob ein Element in IR^n in W liegt, wobei W eine Menge mit m Zusammenhangskomponenten ist.
Der Elementtest benötigt im linearen Modell log(m) Schritte.
ε-closeness benötigt Θ(n log n) Zeit. Denn es ist auf das Elementproblem mit n! Komponenten zurückzuführen.
element uniqueness benötigt Θ(n log n) Zeit. Beweis ähnlich.
Prinzip der Reduktion.
Im linearen Modell benötigt Sortieren Θ(n log n) Zeit.
Beweis durch Reduktion: Falls Sortieren schneller geht, sortiere man und kann dann in linearer Zeit das ε-closeness-Problem lösen. Widerspruch.
all nearest neighbors benötigt Ω(n log n) Zeit.
Beweis durch Reduktion von
ε-closeness auf all nearest neighbors.
KE 2 - Sweep-Verfahren
Sweep-Verfahren
Beispiele:
Bestimung des Maximums einer Zahlenmenge
dichtestes Paar einer Zahlenmenge
maximale Teilsumme einer Zahlenreihe (Aktienkurs)
Dichtestes Punktepaar in der Ebene
Verfahren:
Sweepline läuft entlang einer Achse.
SSS (Sweep-Status-Struktur) enthält alle aktuellen Objekte und Eigenschaften.
ES (Ereignisstruktur) enthält alle Ereignisse, die noch zu durchlaufen sind, sortiert nach der Achsenkoordinate.
Schnittpunkte von Liniensegmenten
Untere Kontur
Durchschnitt von zwei Polygonen
Sweep im Raum
KE 3 - Konvexe Hülle und Sichtbarkeit
Definition konvexe Hülle
Untere Schranke Ω(n log n).
Beweis: Sortierproblem kann auf Konstruktion der konvexen Hülle reduziert werden.
Inkrementelles Verfahren
Es werden nacheinander Punkte hinzugenommen und die Hülle korrigiert.
Randomisierung, damit die Zeit n log n eingehalten wird.
Divide and Conquer
Es werden jeweils zwei Hüllen vereinigt.
Konturpolygon-Verfahren
Mit Sweepline-Verfahren. Vier Streckenzüge bestimmen, die monoton sind. Diese dann korrigieren.
Berechnung der unteren Kontur mit Dualen
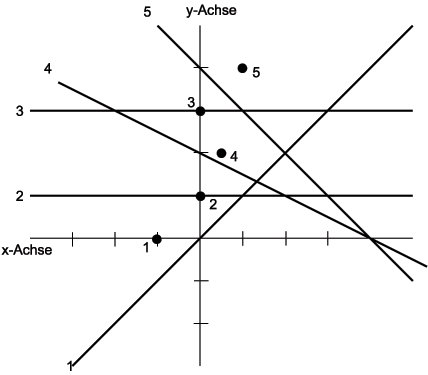
| Gerade | Gleichung | Punkt | Koordinaten |
| 1 | 1*x+0 | 1 | (-1;0) |
| 2 | 0*x+1 | 2 | (0;1) |
| 3 | 0*x+4 | 3 | (0;4) |
| 4 | -0,5*x+3 | 4 | (0,5;3) |
| 5 | -1*x+5 | 5 | (1;5) |
Konstruktion des Sichtbarkeitspolygons
Mit Sweep den Rand durchlaufen und die sichtbaren Bereiche bestimmen.
Kern eines einfachen Polygons
KE 4 - Triangulation
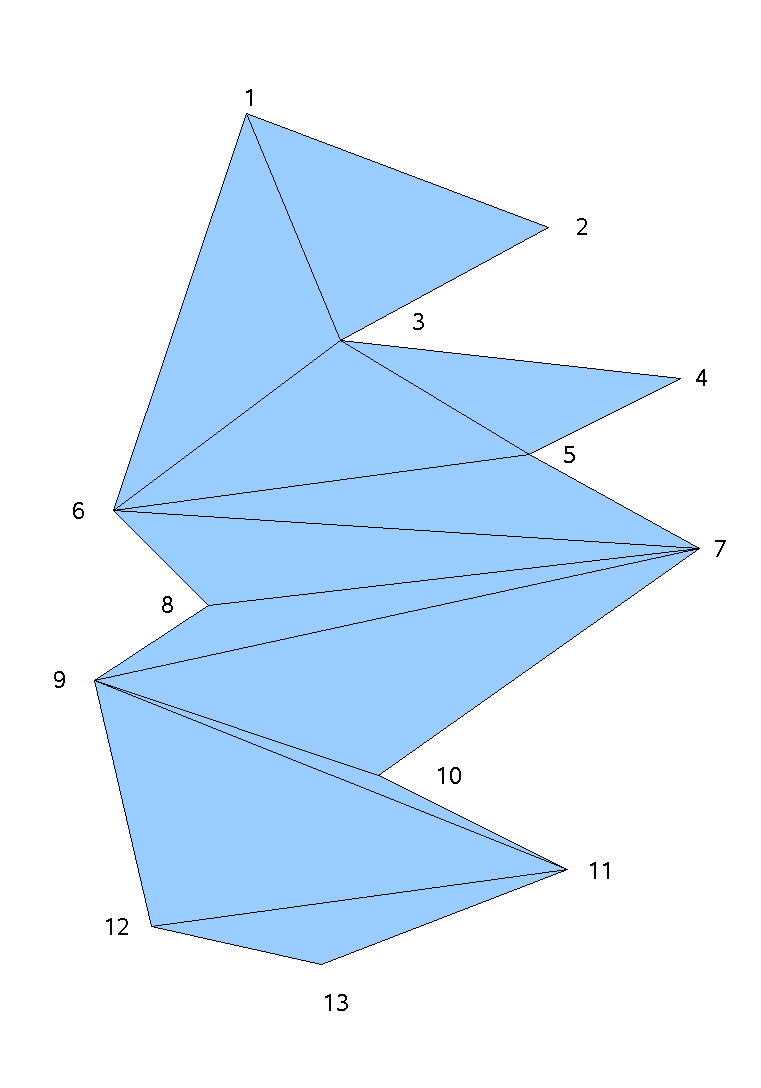 |
S=(1,2) |
Einfache Polygone können in monotone zerlegt werden.
Wächterproblem
Geometrische Datenstrukturen
k-d-Baum
Bereichsbaum
Prioritätssuchbaum
KE 5 - Voronoi-Diagramme
Voronoi-Diagramme
Bisektor
Delaunay-Triangulation
ist dualer Graph zum Voronoi-Diagramm
Voronoi-Diagramme von Liniensegmenten
Bewegungsplanung für Roboter
KE 6 - Berechnung von Voronoi-Diagrammen
Inkrementelle Konstruktion mit Delaunay-DAG
Sweepline mit Wellenfront (Parabeln)
Divide and Conquer (Vernähen der Teillösungen)
Geometrische Transformation (Projektion auf ein Paraboloid)
KE 7 - Bewegungsplanung
Ausweg aus Labyrinth: Plegde-Algorithmus
Zielpunkt finden: Bug-Strategie.
Wanze läuft um Hindernis und sucht Punkt mit kleinstem Abstand zum Ziel. Von dort wird das Hindernis mit Richtung Ziel verlassen.
Bin packing mit first-fit-Strategie. Ist kompetitiv mit Faktor 2.
Suche nach Tür an der Wand. Suchweg in jede Richtung jedesmal verdoppeln. Ist kompetitiv mit Faktor 9.
Suche nach dem Kern eines Polygons: CAB (continuous angular bisector)