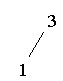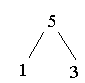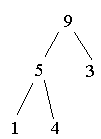Models of
Computation
1.1 Algorithms and
their Complexity
1.2 Random Access
Machines
RAM hat 3 Adressierungsarten (=i, i, *i)
1.3 Computational
Complexity of RAM Programs
worst-case, best-case and expected complexity.
uniform and logorithmic cost criterion.
space and time complexity
1.4 A stored Program
Model
RASP speichert Programm im RAM. Indizierte Adressierung muß simuliert werden.
Beispiel entsprechend Fig. 1.13: SUB *302 muß durch eine RASP simuliert werden. Falls die Daten bei Adresse 300 beginnen, läge das Register bei einer RAM an Stelle 2. Hier sieht die Situation so aus:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
... |
|
3 |
|
4 |
|
9 |
|
|
|
|
|
|
|
|
|
|
Es wird vom Akku-Inhalt in Zelle 0 der Inhalt der Zelle 4 subtrahiert, weil die Zelle 2 auf Zelle 4 verweist. Im Akku steht danach die Zahl -6:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
... |
|
-6 |
|
4 |
|
9 |
|
|
|
|
|
|
|
|
|
|
Bei der RASP-Simulation sieht die Situation so aus:
|
0 |
1 |
2 |
... |
100 |
... |
110 |
111 |
... |
300 |
301 |
302 |
303 |
304 |
... |
|
3 |
|
|
|
3 |
|
6 |
|
|
|
|
4 |
|
9 |
|
Nach dem Befehl STORE 1 (rettet Akku-Inhalt):
|
0 |
1 |
2 |
... |
100 |
... |
110 |
111 |
... |
300 |
301 |
302 |
303 |
304 |
... |
|
3 |
3 |
|
|
3 |
|
6 |
|
|
|
|
4 |
|
9 |
|
Nach dem Befehl LOAD 302 (r=300):
|
0 |
1 |
2 |
... |
100 |
... |
110 |
111 |
... |
300 |
301 |
302 |
303 |
304 |
... |
|
4 |
3 |
|
|
3 |
|
6 |
|
|
|
|
4 |
|
9 |
|
Nach dem Befehl ADD =300 (korrigiert Adresse im Akku):
|
0 |
1 |
2 |
... |
100 |
... |
110 |
111 |
... |
300 |
301 |
302 |
303 |
304 |
... |
|
304 |
3 |
|
|
3 |
|
6 |
|
|
|
|
4 |
|
9 |
|
Nach dem Befehl STORE 111 (schreibt Adresse in den SUB-Befehl):
|
0 |
1 |
2 |
... |
100 |
... |
110 |
111 |
... |
300 |
301 |
302 |
303 |
304 |
... |
|
304 |
3 |
|
|
3 |
|
6 |
304 |
|
|
|
4 |
|
9 |
|
Nach dem Befehl LOAD 1 (stellt den Akku wieder her):
|
0 |
1 |
2 |
... |
100 |
... |
110 |
111 |
... |
300 |
301 |
302 |
303 |
304 |
... |
|
3 |
3 |
|
|
3 |
|
6 |
304 |
|
|
|
4 |
|
9 |
|
Nach dem Befehl SUB 304 (in den Zellen 110 und 111):
|
0 |
1 |
2 |
... |
100 |
... |
110 |
111 |
... |
300 |
301 |
302 |
303 |
304 |
... |
|
-6 |
3 |
|
|
3 |
|
6 |
304 |
|
|
|
4 |
|
9 |
|
1.5 Abstractions of
the RAM
Straight-line programs
bitwise computations
bit vector operations
decision trees
1.6 The Turing
Machine
1.7 Relationship
between TM and RAM
TM, RAM und RASP sind polinomial related.
1.8 Pidgin-Algol
Design of
efficient algorithms
2.1 Data Structures:
Lists, Queues and Stacks
2.2 Set
representations
list, bit vector
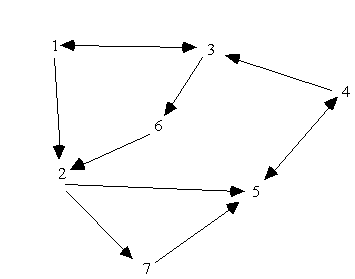
2.3 Graphs
Darstellung durch Adjazenzmatrix oder Adjazenzlisten oder Tabelle.
Beispiel:
2.4 trees
Binärbäume durch zwei Arrays der Söhne darstellbar.
Durchlauf in preorder, postorder oder inorder.
2.5 Rekursion
Jeder rekursive Algorithmus läßt sich mit einem Stack nichtrekursiv programmieren.
2.6
Divide-and-Conquer
Beispiel: Prozedur Maxmin hat den Aufwand
T(n)=. Die Funktion T(n)=3/2*n-2 ist eine Lösung und besser als der Aufwand 2*n, falls man Min und Max getrennt sucht.
Allgemeine Abschätzung für den Aufwand:
Sei T(1)=b
und T(n)=aT(n/c)+bn für n>1.
Dann gilt T(n)=.
Beweis: T(1)=b
T(c)=aT(1)+bc=ab+bc
T(c2)=aT(c)+bc=aab+abc+bcc
T(c3)=aT(c2)+bc=aaab+aabc+abcc+bccc
=bccc(aaa/ccc+aa/cc+a/c+1)
Allgemein gilt T(n)=bn , mit r=a/c.
Falls a<c, konvergiert die unendliche Reihe, also gilt T(n)≤bnk mit einer Konstanten k.
Falls a=c gilt T(n)= bn = bn = bn logn = O(n logn).
Falls a>c gilt T(n)= bn = bn ) =O(nloga).
2.7 Balancing
Mergesort mit Rekursionsgleichungen. Hier ist es wichtig. daß die Teillisten, die gemergt werden, gleich groß sind. Andernfalls wächst der Aufwand.
2.8 Dynamic
Programming
Rekursives Programmieren mit Tabelleneinträgen, um Mehrfachberechnungen zu vermeiden. Beispiel Berechnung der günstigsten Reihenfolge bei der Multiplikation mehrerer Matrizen.
Beispiel: M=[10,50]¥[50,50]¥[50,20]¥[20,10]¥[10,20]
|
m11=0 |
m22=0 |
m33=0 |
m44=0 |
m55=0 |
|
m12 =10*50*50 =25000 |
m23 =50*50*20 =50000 |
m34 =50*20*10 =10000 |
m45 =20*10*20 =4000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sorting and Order
Statistics
3.1 The Sorting
Problem
Internes und Externes Sortieren.
O(n logn) ist die beste Komplexität.
n Elemente zwischen 0 und m-1 lassen sich in O(n+m)-time sortieren.
Strings werden zeitlich proportional zu der Summe der Länge der Strings sortiert.
3.2 Radix Sorting
bucket sort in O(m+n)-time.
lexikogr Sortieren in O((m+n)k)-time, k Länge der Strings, m Größe des Alphabets.
lexikogr Sortieren verschieden langer Strings in O( +m)-time, li Länge der Strings, m Größe des Alphabets.
Anwendung: Isomorphie von Bäumen feststellen.
3.3 Sorting by
Comparisons
Es werden mindestens logn! Vergleiche gebraucht.
Beweis mit Entscheidungsbaum. Der Baum hat n! Blätter. Seine Höhe beträgt somit log(n!)=O(n logn).
Denn n!≥n(n-1)...(n/2)≥(n/2)n/2
Hieraus folgt logn!≥log((n/2)n/2)≥n/2 log(n/2)=n/4 log(n).
3.4 Heap-Sort
(O(nlogn)-Algorithmus)
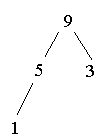
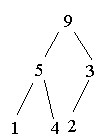
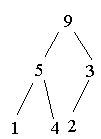
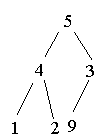
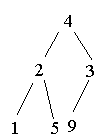
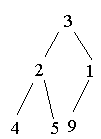
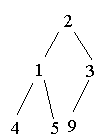
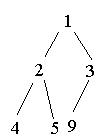
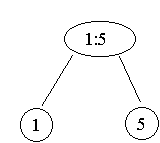
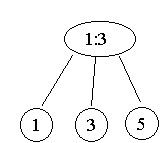
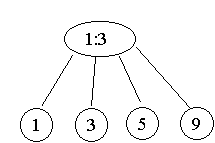
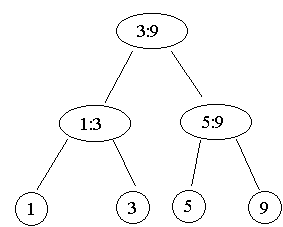
Heap aufbauen: (3 1 5 9 4 2)
Heap abbauen:
3.5 Quicksort - An
O(n logn) expected time sort
Beispiel durchgehen, Komplexität berechnen (S.94)
3.6 Order Statistics
Finden des k-größten Elements in einer unsortierten Liste.
T(n)≤cn für n≤49
T(n)≤T(n/5)+T(3n/4)+cn für n≥50.
Durch Induktion ergibt sich T(n)≤20cn.
3.7 Expected Time for
Order Statistics
Hier ergibt sich im Durchschnitt T(n)≤4cn.
Data Structures
for Set Manipulation Problems
4.1 Fundamental
Operations on Sets
online - offline, welche Bedeutung
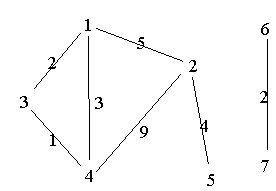
Beispiel: Spanning tree, Kruskals Algorithmus
4.2 Hashing
Mit hash-Funktion h(m)=m mod n.
Für Sortierung eventuell Zusatzstruktur aufbauen.
4.3 Binary Search
mit sortierter Liste, INSERT aufwendig
4.4 Binary Search
Trees
Aufwand berechnen (expected time):
T(n)=1/n = n-1+2/n ≤ kn logn mit den Mitteln von Abschnitt 3.5 (machen!).
4.5 Optimal Binary
Search Trees
mit dynamischer Programmierung (Beispiel S.122)
Beispiel: Einen optimalen binären Suchbaum berechnen.
Werte mit Zugriffswahrscheinlichkeiten:
|
|
2 |
|
7 |
|
10 |
|
15 |
|
18 |
|
|
0,1 |
0,3 |
0,01 |
0,1 |
0,09 |
0,1 |
0,1 |
0,1 |
0,02 |
0,05 |
0,03 |
|
q0 |
p1 |
q1 |
p2 |
q2 |
p3 |
q3 |
p4 |
q4 |
p5 |
q5 |
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
0 |
w00=0,1 c00=0 |
w11=0,01 c11=0 |
w22=0,09 c22=0 |
w33=0,1 c33=0 |
w44=0,02 c44=0 |
w55=0,03 c55=0 |
|
1 |
w01=0,41 c01=0,41 r01=2 |
w12=0,2 c12=0,2 r12=7 |
w23=0,29 c23=0,2 r23=10 |
w34=0,22 c34=0,22 r34=15 |
w45=0,1 c45=0,1 r45=18 |
|
|
2 |
w02=0,6 c02= r02= |
w13=0,4 c13= r13= |
w24=0,41 c24= r24= |
w35=0,3 c35= r35= |
|
|
|
3 |
w03= c03= r03= |
w14= c14= r14= |
w25= c25= r25= |
|
|
|
|
4 |
w04= c04= r04= |
w15= c15= r15= |
|
|
|
|
|
5 |
w05= c05= r05= |
|
|
|
|
|
4.6 A Simple
Disjoint-Set Union Algorithm
Das Universum ist klein.
n Union in O(n logn) und n FIND in O(n) time.
siehe Fig 4.13 und 4.15
4.7 Tree Structures
for the Union-Find-Problem
Union durch Verschmelzen von Bäumen.
Zum Ausbalancieren den kleineren Baum zum Sohn der Wurzel des größeren Baumes machen.
Durch path compression bei jedem FIND(i) wesentliche Beschleunigung.
4.8 Applications and
Extensions of the Union-Find Algorithm
Offline-Min Problem
Depth determination problem
Equivalence of finite
Automata
Beispiel: c und c´ Startzustände, g und g´ Endzustände.
A: A´:
d 0 1 d 0 1
a b g a´ a´ g´
b b g c´ e´ g´
c e g d´ e´ a´
d f b e´ e´ c´
e e c g´ a´ e´
f f d
g a f
4.9 Balanced Tree
Schemes
2-3 trees
Aufbauen (1 5 3 9 4 2 6 8)
Abbauen ebenfalls machen.
Datenstrukturen mit ihren Operationen:
1) dictionary (INSERT, DELETE, MEMBER)
2) priority queue (INSERT, DELETE, MIN)
3) mergeable heap (INSERT, DELETE, UNION, MIN)
4) concatenable queue (INSERT, DELETE, FIND, CONCATENATE, SPLIT)
4.10 Dictionaries and
priority queues
In 2-3-Bäumen können n INSERT, DELETE und MIN in O(n logn) Zeit vorgenommen werden.
4.11 Mergeable Heaps
Es sollen n INSERT, DELETE, UNION und MIN in O(n logn) Zeit durchgeführt werden. Zur Darstellung werden unsortierte 2-3-Bäume verwendet, deren Knoten mit dem Wert Smallest(v) versehen werden. Ein weiterer 2-3-Baum wird benutzt, um beliebige Werte in O(logn) Zeit finden zu können. UNION wird mit der Prozedur IMPLANT realisiert.
4.12 Concatenable
queues
Wie in 4.10 werden 2-3-Bäume verwendet, um INSERT, DELETE, MIN, MEMBER und zusätzlich CONCATENATE und SPLIT in O(logn) Zeit zu realisieren. Konkatenieren mit der Prozedur IMPLANT. SPLIT erzeugt links und rechts des Pfades zum Element lauter Teilbäume, die mit IMPLANT zu zwei neuen Bäumen zusammengefaßt werden.
4.13 Partitioning
****************************************
Technik: Für jeden Block B[i] f-1(B[i]) berechnen. Für jeden Block B[j], der das Urbild schneidet, zwei Blöcke erzeugen.
Anwendung: Minimalen Automaten erzeugen. Siehe Aufg 3.4
Beispiel (Aufg. 3.4): Sei A=({a,b,c,d,e,f,g},{0,1},d,c,{e,f}) mit
|
d |
0 |
1 |
|
a |
b |
g |
|
b |
b |
g |
|
c |
e |
g |
|
d |
f |
b |
|
e |
e |
c |
|
f |
f |
d |
|
g |
a |
f |
Errechne einen minimalen Automaten.
Algorithms on Graphs
5.1 Minimale
Spannbäume
Kruskals Algorithmus, Aufwand O(e loge) für Sortierung.
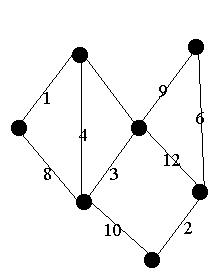
5.2 Tiefensuche
Ein ungerichteter Graph wird aufgeteilt in einen Baum (tree) und in back edges. O(max(n,e)) Aufwand.
5.3 Bikonnektivität
Algorithmus: es werden die Konzentrationspunkte (articulation points) gefunden.
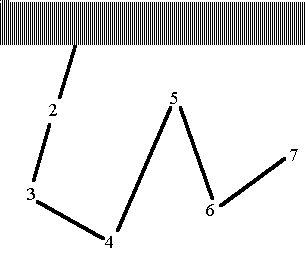
5.4 Tiefensuche eines
gerichteten Graphen
Es gibt neben den tree edges forward edges, back edges und cross edges.
5.5 Strong
Connectivity
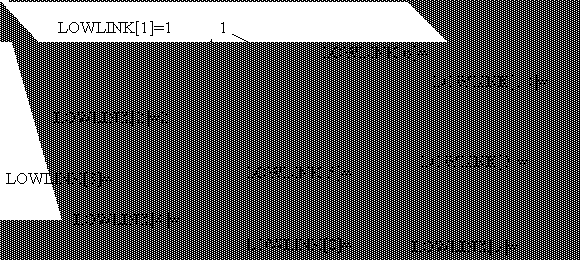
Im Verfahren sind die Knoten i mit LOWLINK(i)=i die Wurzeln von strongly connected components. Algorithmus Fig 5.15 machen.
Beispiel:

5.6 Path-finding
problems
Semiringe, Kosten von Pfaden mit Algorithmus 5.5.
S1 zum Finden von Wegen, S2 zum Finden der minimalen Kosten von Wegen.
5.7 A transitive
Closure Algorithm
Mit Alg 5.5 und Semiring S1.
Beispiel:
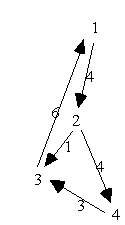
5.8 A shortest-path
algorithm
Mit Alg 5.5 und Semiring S2.
5.9 Path Problem and
Matrix Multiplication
Abschluß durch berechnen.
Multiplikation nicht schwerer als Berechnung des Abschluß. Beweisidee:
Sei X= ). Dann gilt X*=I+X+X2= ).
Abschluß ebenfalls nicht schwerer zu berechnen als Multiplikation.
5.10 Single-Source
Problems
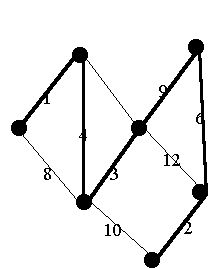
Kürzeste Pfade von einem Knoten zu allen anderen berechnen. Mit Dijkstras Algorithmus.
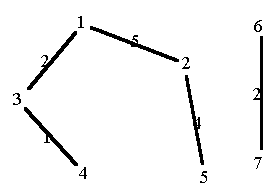
Beispiel: Berechne alle kürzesten Entfernungen von Knoten 1 aus.
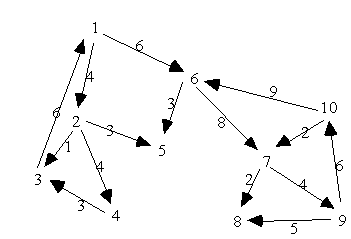
Lösung:
|
S |
w |
D(w) |
D(1) |
D(2) |
D(3) |
D(4) |
D(5) |
D(6) |
D(7) |
D(8) |
D(9) |
D(10) |
|
1 |
- |
- |
0 |
4 |
∞ |
∞ |
∞ |
6 |
∞ |
∞ |
∞ |
∞ |
|
1,2 |
2 |
2 |
0 |
4 |
5 |
8 |
7 |
6 |
∞ |
∞ |
∞ |
∞ |
|
1,2,3 |
3 |
5 |
0 |
4 |
5 |
8 |
7 |
6 |
∞ |
∞ |
∞ |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.11 Dominatoren
Matrixmultiplikation
6.1 Basics
6.2 Strassens
Matrix-Multiplication Algorithm
) ) = )
Wegen 7 Multiplikationen gilt T(n)=7T(n/2)+18(n/2)2 ≤ O(nlog7) ≈ O(n2,81).
6.3 Invertierung von
Matrizen
Invertierung von Dreiecksmatrizen nicht schwieriger als Multiplikation.
6.4 LUP Decomposition
of matrices
A=L U P. Dann folgt
A x=b fi L U P x=b fi L y=b fi U P x=y fi U z=y fi P x=z fi x=P-1 z
6.5 Applications of
LUP Decomposition
Determinanten in O(n2,81)
Simultane Gleichungen auflösen in O(n2,81)
Invertierung in O(n2,81)
6.6 Boolean Matrix
Multiplication
Erstes Verfahren: Rechnen im Ring ZZn+1,
dann Übergang zu booleschen Werten. Aufwand OB(n2,81 m(logn)), wobei m(k) der Aufwand der
Multiplikation von k-bit integers ist. Da m(k)=O(k logk loglogk), folgt der
Aufwand OB(n2,81 logn loglogn logloglogn).
Vier Russen:
Beispiel:
|
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
x |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
Vorausberechnung für A1*B1:
ROWSUM(0)=(0,0,0,0)
ROWSUM(1)=(0,1,0,0)
ROWSUM(2)=(0,1,1,0)
ROWSUM(3)=(0,1,1,0)
C1:
|
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
Vorausberechnung für A2*B2:
ROWSUM(0)=(0,0,0,0)
ROWSUM(1)=(0,0,1,1)
ROWSUM(2)=(1,1,1,0)
ROWSUM(3)=(1,1,1,1)
C2:
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
Addition von C1 und C2:
|
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
+ |
1 |
1 |
1 |
0 |
= |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
0 |
Aufwand O(n3/logn).
7.1 The discrete
Fourier Transform and its inverse
w ist die n-te primitive Einheitswurzel, wenn gilt w≠1, wn=1 und
=0 für 1≤p<n.
Beispiel: ei2p/n.
F(a)=Aa mit A(i,j)=wij ist die Fouriertransformierte von a.
Die Inverse ist gegeben durch A-1 mit A-1(i,j)=1/n w-ij.
Konvolution: a *O b=c mit ci= .
Konvolutionstheorem: a *O b= F-1(F(a).F(b)).
Wrapped convolution: (n=4)
c0=a0b0+a1b3+a2b2+a3b1
c1=a0b1+a1b0+a2b3+a3b2
c2=a0b2+a1b1+a2b0+a3b3
c3=a0b3+a1b2+a2b1+a3b0
d0=a0b0-a1b3-a2b2-a3b1
d1=a0b1+a1b0-a2b3-a3b2
d2=a0b2+a1b1+a2b0-a3b3
d3=a0b3+a1b2+a2b1+a3b0
p0=(c0+d0)/2
p1=(c1+d1)/2
p2=(c2+d2)/2
p3=(c3+d3)/2
p4=(c0-d0)/2
p5=(c1-d1)/2
p6=(c2-d2)/2
p7=(c3-d3)/2=0
7.2 The Fast Fourier
Transform Algorithm
Anstatt ein Polynom p an der Stelle a auszuwerten, kann man auch den Rest bei Division durch x-a berechnen, denn aus p(x)=(x-a)q(x)+c mit c als Rest folgt bei Einsetzen von a p(a)=(a-a)q(x)+c=c, also c=a. Dies gilt auch für wiederholte Divisionen: Sei p(x)=(x-a)(x-b)q(x)+r(x) und r(x)=(x-b)s(x)+c. Bei Einsetzen von b gilt p(b)=(b-a)(b-b)q(b)+r(b) und r(b)=(b-b)s(b)+c, also r(b)=c, also p(b)=(b-a)(b-b)q(b)+c=c.
Bei dem schnellen Algorithmus 7.1 wird das Polynom durch die eine Hälfte der Terme x-wi geteilt, dann durch eine weitere Hälfte dieser Terme usw. Dadurch muß nicht immer wieder das ganze Polynom dividiert werden. Ferner können die Terme x-wi so gewählt werden, daß der Dividend immer die Form xs-wj hat.
Der Algorithmus 7.1 benötigt OA(n logn) Zeit.
7.3 The FFT Using Bit
Operations
Wenn n und w Potenzen von 2 sind, ist w eine primitive n-te Einheitswurzel des Ringes Rm mit m=wn/2+1.
Das Konvolutionstheorem läßt sich anwenden auf den Ring der Zahlen modulo 2n/2+1. Die Zahlen müssen dann im Bereich o bis 2n/2 liegen, damit das Ergebnis exakt ist.
7.4 Products of
Polynomials
Der Algorithmus 7.1 gilt wie für Vektoren auch für Polynome. Somit läßt sich das Produkt zweier Polynome mit Grad n in OA(n logn) Zeit berechnen.
7.5 The
Schönhage-Strassen Algorithm
Der Schönhage-Strassen Algorithmus teilt die Integerzahlen in gleichgroße Blöcke auf und wendet darauf das Konvolutionstheorem an. Es müssen noch anders als bei Polynomen die Überträge berücksichtigt werden.
Integer and Polynomial Arithmetic
8.1 Similarity
between Integers and Polynomials
8.2 Integer
Multiplication and Division
Abkürzungen: M(n) Zeit für Integermultiplikation
D(n) Zeit für Integerdivision
S(n) Zeit für Integerquadrierung
R(n) Zeit für Berechnung des Integerkehrwertes
Der Kehrwert kann mit dem Algorithmus Reciprocal berechnet werden, der auf der Gleichung Ai+1=2Ai-Ai2P beruht. Es gilt R(n)≤cM(n).
S(n)≤cR(n). Beweis mit der Gleichung P2= ) - )) -P.
M(n), R(n), D(n) und S(n) unterscheiden sich nur durch konstante Faktoren.
Beweis: R(n)≤cM(n) und S(n)≤cR(n) sind schon bewiesen. M(n)≤c(S(n) ergibt sich aus AB=1/2((A+B)2-A2-B2). R(n)≤cD(n) ist trivial. D(n)≤cR(n) ergibt sich aus der Beziehung A/B=A*(1/B).
8.3 Polynomial
Multiplication and Division
8.4 Modular
Arithmetic
Sind die Zahlen p0,...,pk-1 relativ prim zueinander und gilt 0≤u<p, so besteht zwischen u und den Resten u0,...,uk-1 ein Isomorphismus, ausgedrückt durch
u´(u0,...,uk-1).
Man kann mit den Resten rechnen:
u+v´(u0+v0,...,uk-1+vk-1)
u-v´(u0-v0,...,uk-1-vk-1)
u*v´(u0*v0,...,uk-1*vk-1)
Division läßt sich leider nicht mit modularer Arithmetic realisieren.
Berechnung der Reste wieder durch Divide-and-conquer.
Beispiel: Berechne die Reste von 53 bezüglich (2,5,7,11). Das Ergebnis ist (1,3,4,9).
53=3 mod 10 und 53=53 mod 77.
3=1 mod 2 und 3=3 mod 5.
53=4 mod 7 und 53=9 mod 11.
8.5 Modular
Polynomial Arithmetic and Polynomial Evaluation
Analog kann man bei Polynomen vorgehen.
Beispiel: p(x)=8x^3+4x^2-8x+6. Seien p0(x)=x-2, p1(x)=x^2+2, p2(x)=x+2, p3(x)=x. Dann gilt
p/(x-2)=70
p/x^2+2=-2 - 24 x
p/x+3=-150
p/x=6
q1=p/((x-2)*(x^2+2))=38 - 24 x + 20 x
q2=p/((x+2)*x)=6 + 16 x
q1/(x-2)=70
q1/(x^2+2)=-2 - 24 x
q2/(x+2)=-26
q2/x=6
8.6 Chinese
Remaindering
8.7 Chinese
Remaindering and Interpolation of Polynomials
8.8 Greatest Common
Divisors and Euclid´s Algorithm
Mit dem Euklidischen Algorithmus kann man nicht nur den GCD zweier Zahlen a0 und a1, sondern auch die Zahlen x und y berechnen, für die a0x+a1y=GCD(a0,a1) gilt:
x0:=1; y0:=0; x1:=0; y1:=1; i:=1;
while ai does not divide ai-1 do begin
q:=int(ai-1/ai);
ai+1:=ai-1-q*ai;
xi+1:=xi-1-q*xi;
yi+1:=yi-1-q*yi;
i:=i+1;
end;
Beispiel:
|
i |
ai |
xi |
yi |
q |
|
0 |
140 |
1 |
0 |
|
|
1 |
82 |
0 |
1 |
1 |
|
2 |
58 |
1 |
-1 |
1 |
|
3 |
24 |
-1 |
2 |
2 |
|
4 |
10 |
3 |
-5 |
2 |
|
5 |
4 |
-7 |
12 |
2 |
|
6 |
2 |
17 |
-29 |
|
Also gilt GCD(140,82)=2 und 17*140+(-29)*82=2380-2378=2=GCD(140,82).
8.9 An Asymptotically
Fast Algorithm for Polynomial GCD´s
Es ist eine Abwandlung des Euklidischen Algorithmus. Vor allem wird zu Anfang in HGCD nur die erste Hälfte der Polynome berücksichtigt.
8.10 Integer GCD´s
Der Algorithmus HGCD kann nach Anpassung auf Integers angewendet werden.
8.11 Chinese
Remaindering revisited
Im Divide-and-Conquer-Algorithmus mußten die Werte di=ei-1=(p/pi)-1 zur Verfügung gestellt werden. Sie können aber mit einem abgewandelten GCD-Algorithmus berechnet werden, denn aus eix+piy=1 folgt eix=1 mod pi und damit x=ei-1=di mod pi.
Theorem 8.21: Seien k Reste mit jeweils b bits gegeben, so benötigt das Chinese Remaindering OB(M(bk) log k)+OB(k M(b) log b) Schritte.
Korollar: Chinese Remaindering without preconditioning erfordert höchstens OB(bk log2 bk loglog bk).
8.12 Sparse
Polynomials
Schwach besetzte Polynome werden durch Folgen von (ai,ji) dargestellt.
Seien f(x) durch (a1,j1),...,(am,jm) und g(x) durch (b1,k1),...,(bn,kn) gegeben.
Bilde für 1≤i≤n die Mengen Si mit allen Elementen (arbi,jr+ki) mit 1≤r≤m.
Merge dann nebeneinander stehende Mengen Si und Si+1 solange, bis eine sortierte Menge übrigbleibt.
Beispiel: f(x)=x7+2x+1 ist gegeben durch (1,7),(2,1),(1,0) und
g(x)=4x6-2x2+1 durch (4,6),(-2,2),(1,0).
S0={(1,0),(2,1),(1,7)}
S2={(-2,2),(-4,3),(-2,9)}
S6={(4,6),(8,7),(4,13)}
Mergen der Mengen S0 und S2 ergibt
S0,2={(1,0),(2,1),(-2,2),(-4,3),(1,7),(-2,9)}.
Mergen mit S6 ergibt
S0,2,6={(1,0),(2,1),(-2,2),(-4,3),(4,6),(9,7),(-2,9),(4,13)}.
Der Aufwand beträgt O(mn logn) Zeit, wobei m≥n angenommen wird.