Parallele Algorithmen
KE 2
Übertragsvorausberechnung
Beispiel:
i |
5 |
4 |
3 |
2 |
1 |
0 |
Stelle |
xi |
1 |
1 |
0 |
0 |
1 |
Bits der ersten Zahl |
|
yi |
1 |
0 |
0 |
1 |
1 |
Bits der zweiten Zahl |
|
si |
2 |
1 |
0 |
1 |
2 |
Summen |
|
Si |
0 |
2 |
0 |
0 |
2 |
2 |
Präfixsummen der si bezüglich der Operation · |
ci |
0 |
1 |
0 |
0 |
1 |
1 |
Überträge für die nächste Stelle |
xi |
1 |
1 |
0 |
0 |
1 |
Bits der ersten Zahl |
|
yi |
1 |
0 |
0 |
1 |
1 |
Bits der zweiten Zahl |
|
c(i+1) |
1 |
0 |
0 |
1 |
1 |
0 |
Überträge nach links verschoben |
zi |
1 |
0 |
1 |
1 |
0 |
0 |
Summe |
Präfixsummen
Beispiel:
| Stelle | 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Zahl | 2 |
4 |
3 |
8 |
1 |
3 |
2 |
6 |
|
Rekusion |
6 |
11 |
4 |
8 |
||||
|
17 |
12 |
|||||||
29 |
||||||||
17 |
29 |
|||||||
6 |
17 |
21 |
29 |
|||||
Präfixsummen |
2 |
6 |
9 |
17 |
18 |
21 |
23 |
29 |
KE 3
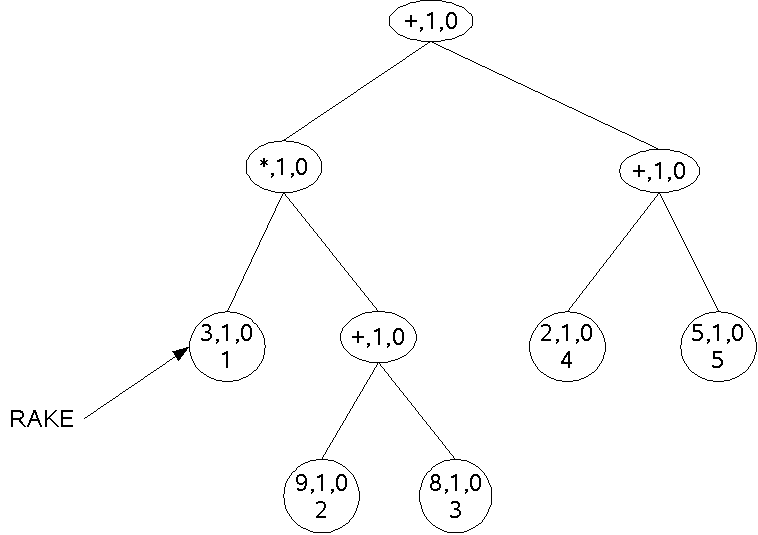
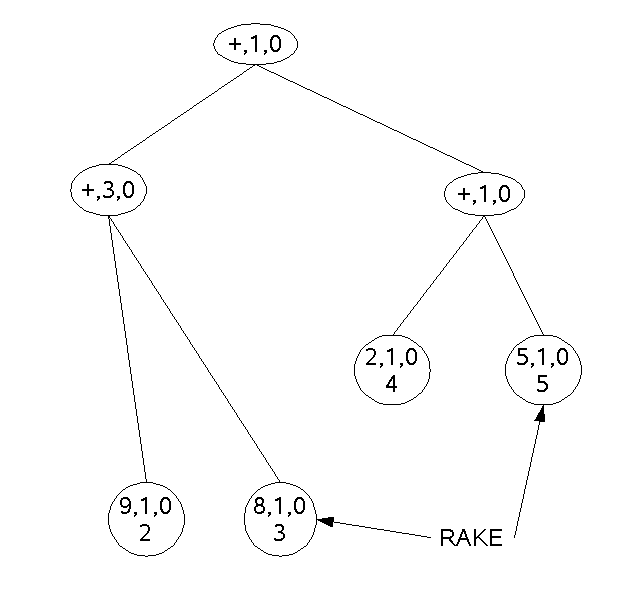
Rake
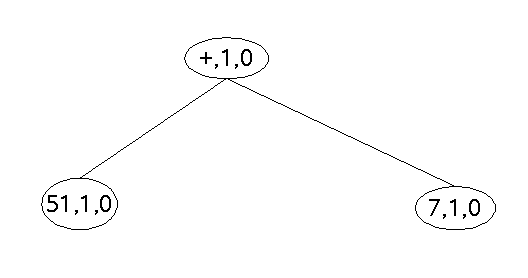
Beispiel: (3*(9+8))+(2+5)=3*17+7=51+7=58
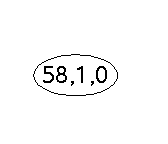
KE 5
Fourier Transformation
Polynomdivision
KE 6
Paralleles Merging
Beispiel:
Stelle |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|||
A |
1 |
3 |
5 |
9 |
14 |
16 |
17 |
20 |
21 |
22 |
30 |
31 |
40 |
42 |
43 |
45 |
|||
B |
3 |
4 |
8 |
11 |
13 |
18 |
19 |
21 |
25 |
26 |
28 |
30 |
32 |
35 |
37 |
50 |
n=m=16
log(n)=4
Stelle |
1 |
2 |
3 |
4 |
B(1) |
3 |
4 |
8 |
11 |
B(2) |
13 |
18 |
19 |
21 |
B(3) |
25 |
26 |
28 |
30 |
B(4) |
32 |
35 |
37 |
50 |
r1 = rank(3 : A) = 1
r2 = rank(13 : A) = 4
r3 = rank(25 : A) = 10
r4 = rank(32 : A) = 12
Stelle |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
5 |
6 |
||
B(1) |
3 |
4 |
8 |
11 |
A(1) |
3 |
5 |
9 |
||||
B(2) |
13 |
18 |
19 |
21 |
A(2) |
14 |
16 |
17 |
20 |
21 |
22 |
|
B(3) |
25 |
26 |
28 |
30 |
A(3) |
30 |
31 |
|||||
B(4) |
32 |
35 |
37 |
50 |
A(4) |
40 |
42 |
43 |
45 |
A(2) ist zu groß, deshalb Algorithmus nochmal auf A(2) und B (2) anwenden.
Stelle |
1 |
2 |
3 |
4 |
5 |
6 |
A(2) |
14 |
16 |
17 |
20 |
21 |
22 |
B(2) |
13 |
18 |
19 |
21 |
n=6 m=4
log(m)=2
Stelle |
1 |
2 |
B(2)(1) |
13 |
18 |
B(2)(2) |
19 |
21 |
r1 = rank(13 : A(2) ) = 0
r2 = rank(19 : A(2) ) = 3
Stelle |
1 |
2 |
1 |
2 |
3 |
||
B(2)(1) |
13 |
18 |
A(2)(1) |
14 |
16 |
17 |
|
B(2)(2) |
19 |
21 |
A(2)(2) |
20 |
21 |
22 |
Finden des k-ten Elements
Beispiel: Gesucht ist das 10. Element.
| Menge | 3 |
19 |
20 |
5 |
4 |
9 |
7 |
13 |
21 |
2 |
4 |
6 |
1 |
11 |
18 |
| Median | 5 |
9 |
6 |
||||||||||||
|
6 |
|||||||||||||||
| A | Menge aller Zahlen < 6 | |||||
| |A|=6 | 3 |
4 |
5 |
2 |
4 |
1 |
| B | Menge aller Zahlen > 6 | |||||||
| |B|=8 | 19 | 20 | 9 | 7 | 13 | 21 | 11 | 18 |
Gesucht ist das 3. Element in B, da 10-6-1=3.
| Menge | 19 |
20 |
9 |
7 |
13 |
21 |
11 |
18 |
| Median | 13 |
18 |
||||||
13 |
||||||||
| A | Menge aller Zahlen < 13 | ||
| |A|=3 | 9 |
7 |
11 |
| B | Menge aller Zahlen > 13 | |||
| |B|=4 | 19 |
20 |
21 |
18 |
Gesucht ist das 3. Element in A.
| Menge | 9 |
7 |
11 |
| Median | 9 |
||
| A | Menge aller Zahlen < 9 |
| |A|=1 | 7 |
| B | Menge aller Zahlen > 9 |
| |B|=1 |
11
|
Gesucht ist das 1. Element in B, da 3-1-1=1.
Das ist dann die Zahl 11.